Saturday, January 10, 2015

Simple Harmonic Motion an application of differential and Integral Calculus and Periodic Trigonometric functions.


CSAT APTITUDE



 
SHM: Stands for Simple Harmonic Motion .It's most important property is it's total mechanical Energy is conserved during its period of motion ie Sum(dK+dU)=constant .It's knowledge is mandatory to understand electromagnetic Radiation,Spring mass system and Antenna theory thus it is the key to understanding physical layer communication theory. 
The projection of simple harmonic motion along x-axis and y-axis is A Cos(wt+phi) and along y-axis
 A sin(wt+phi)  .
Mathematically, the restoring force F is given by
\mathbf{F}=-k\mathbf{x},
where F is the restoring elastic force exerted by the spring (in SI units: N), k is the spring constant (N·m−1), and x is the displacement from the equilibrium position (in m). This restoring force is responsible for simple harmonic motion.
Equation  for simple harmonic motion.
For one-dimensional simple harmonic motion, the equation of motion, which is a second-order linear ordinary differential equation with constant coefficients, could be obtained by means of Newton's second law (and Hooke's law for a mass on a spring).
F_{net} = m\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -kx,
where m is the inertial mass of the oscillating body, x is its displacement from the equilibrium (or mean) position, and k is the spring constant.
Therefore,
\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -\left(\frac{k}{m}\right)x,
Solving the differential equation above, a solution which is a sinusoidal function is obtained.
x(t) = c_1\cos\left(\omega t\right) + c_2\sin\left(\omega t\right) = A\cos\left(\omega t - \varphi\right),
where
\omega = \sqrt{\frac{k}{m}},
A = \sqrt{{c_1}^2 + {c_2}^2},


\tan \varphi = \left(\frac{c_2}{c_1}\right),
In the solution, c1 and c2 are two constants determined by the initial conditions, and the origin is set to be the equilibrium position. Each of these constants carries a physical meaning of the motion: A is the amplitude (maximum displacement from the equilibrium position), ω = 2πf is the angular frequency, and φ is the phase.[
Using the techniques of differential calculus, the velocity and acceleration as a function of time can be found:
v(t) = \frac{\mathrm{d} x}{\mathrm{d} t} = - A\omega \sin(\omega t-\varphi),
Speed:
{\omega} \sqrt {A^2 - x^2}
Maximum speed = wA (at equilibrium point)
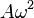a(t) = \frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = - A \omega^2 \cos( \omega t-\varphi).
Maximum acceleration = A\omega^2 (at extreme points)
Acceleration can also be expressed as a function of displacement:
a(x) = -\omega^2 x.\!
Then since ω = 2πf,
f = \frac{1}{2\pi}\sqrt{\frac{k}{m}},
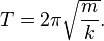
          T = 2\pi \sqrt{\frac{m}{k}}.

 and, since T = 1/f where T is the time period,


The kinetic energy K of the system at time t is
K(t) = \frac{1}{2} mv^2(t) = \frac{1}{2}m\omega^2A^2\sin^2(\omega t - \varphi) = \frac{1}{2}kA^2 \sin^2(\omega t - \varphi),
and the potential energy
U(t) = \frac{1}{2} k x^2(t) = \frac{1}{2} k A^2 \cos^2(\omega t - \varphi).
The total mechanical energy of the system therefore has the constant value
E = K + U = \frac{1}{2} k A^2.
Simple harmonic motion can also be related to circular motion where the centripetal acceleration a=v^2/r =w^2.r is the restoring force acceleration responsible for circular periodic motion as for simple harmonic motion a restoring force towards the origin or center of circle is required.




Like all other motions of an object that can be modeled as a particle, circular motion is governed by Newton’s second law. The object’s acceleration toward the center of the circle must be caused by a force, or several forces, such that their vector sum
SUM(F) is a vector that is always directed toward the center, with constant
magnitude. The magnitude of the radial acceleration is given by 
Circular motion of a mass attached by a thread is an example of simple harmonic motion and its free body diagram is given as following you can work out the conservative restoring force by free body diagram and tell me in the comment!

http://youtu.be/XCyiqKy50AI
http://youtu.be/3zJfcafFdc4

For reference you can see at .http://en.wikipedia.org/wiki/Simple_harmonic_motion.
https://www.youtube.com/watch?v=bmczI-3qSJw&feature=youtu.be 

https://www.youtube.com/watch?v=bmczI-3qSJw&feature=youtu.be
google90d3ff75056c853f.html


http://advancedmathematicalresearch.blogspot.in/
Posted by at

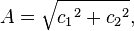
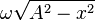
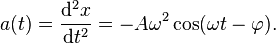
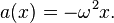
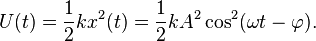
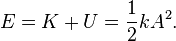
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)