We are going to analyses the flow of an incompressible,non-viscous and non-turbulent ie streamed lined flow of fluid.
The Continuity Equation
The mass of a moving fluid doesn’t change as it flows. This leads to an important quantitative relationship called the continuity equation. Consider a portion of a flow tube between two stationary cross sections with areas A1 and A2.The fluid speeds at these sections are v1 and v2.respectively.During a small time interval dt, the fluid at A1moves a distance v1dt,so a cylinder of fluid with height v1dt and volume dV1 = A1v1dt flows into the tube across A1.During this same interval, a cylinder of volume dV2 = A2v2dt flows out of the tube across A2.Let’s first consider the case of an incompressible fluid so that the density has the same value at all points.The mass dm1 flowing into the tube across A1in time dt is dm1 = rA1v1 dt.Similarly, the mass dm2 that flows out across A2 in the same time is dm2 = rA2v2 dt. In steady flow the total mass in the tube is constant soSo dm1=dm2. and
rA1v1 dt = rA2v2 dt or
A1v1 = A2v2 (continuity equation, incompressible fluid)
The figure illustrating the above derivation
Deriving Bernoulli’s Equation
To derive Bernoulli’s equation, we apply the work–energy theorem to the fluid in a section of a flow tube.And the figure that will assist us in deriving this relation is as following:
Let’s compute the work done on this fluid element during dt. We assume that there is negligible internal friction in the fluid (i.e., no viscosity), so the only nongravitational forces that do work on the fluid element are due to the pressure of the surrounding fluid. The pressures at the two ends are p1 and p2.the force on cross section at a is p1A1 and the force at c is p2A2.The net work dW done on the element by the surrounding fluid during this displacement is therefore
The work dW is due to forces other than the conservative force of gravity, so it equals the change in the total mechanical energy (kinetic energy plus gravitational potential energy) associated with the fluid element. The mechanical energy for the fluid between sections b and c does not change.At the beginning of dt the fluid between a and b has volume A1 ds1, mass rA1 ds1 and kinetic energy
At the end of dt the fluid between c and d has kinetic energy
The net change in kinetic energy dK during time dt is
The net change in potential energy dU during dt is






















 then
then 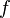 has a local maximum at
has a local maximum at  .
. then
then 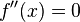 , the test is inconclusive.
, the test is inconclusive.




