Ellipse ,It'a Algebraic and Parametric Equation and Application in physics1: http://t.co/VV0pSNCLKh via @YouTube
— Abraham Malik (@brhmmlk93_malik) February 14, 2015
Today i will start from the definition of circle .The circle is the locus of a point P(x,y) which moves in such a way that it's distance from fixed point called center is constant that constant is called the radius of circle Using this definition we can derive equation of circle using Distance formula from coordinate Geometry.
d=sqrt[(X2-X1)^2 + (Y2-Y1)^2]
A circle is a simple shape in Euclidean geometry. It is the set of all points in a plane that are at a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves so that its distance from a given point is constant. The distance between any of the points and the centre is called the radius.
A circle is a simple closed curve which divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is the former and the latter is called a disk.
A circle may also be defined as a special ellipse in which the two foci are coincident and the eccentricity is 0, or the two-dimensional shape enclosing the most area per unit perimeter, using calculus of variations.
An alternative parametrisation of the circle is:
A common example occurs in kinematics, where the trajectory of a point is usually represented by a parametric equation with time as the parameter.

Adding these two equations together gives:
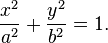
This means any noncircular ellipse is a compressed (or stretched) circle. If a circle is treated like an ellipse, then the area of the ellipse would be proportional to the length of either axis (i.e. doubling the length of an axis in a circular ellipse would create an ellipse with double the area of the original circle).
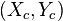 is the center of the ellipse, and
is the center of the ellipse, and 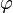 is the angle between the
is the angle between the  -axis and the major axis of the ellipse
-axis and the major axis of the ellipse
d=sqrt[(X2-X1)^2 + (Y2-Y1)^2]
A circle is a simple shape in Euclidean geometry. It is the set of all points in a plane that are at a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves so that its distance from a given point is constant. The distance between any of the points and the centre is called the radius.
A circle is a simple closed curve which divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is the former and the latter is called a disk.
A circle may also be defined as a special ellipse in which the two foci are coincident and the eccentricity is 0, or the two-dimensional shape enclosing the most area per unit perimeter, using calculus of variations.
Cartesian coordinates
n an x–y Cartesian coordinate system, the circle with centre coordinates (a, b) and radius r is the set of all points (x, y) such that

- Is the equation of a circle whose origin is shifted by X=a and Y=b from O(0,0)

- The equation can be written in parametric form using the trigonometric functions sine and cosine as


An alternative parametrisation of the circle is:
Parametric equation
In mathematics, parametric equations of a curve express the coordinates of the points of the curve as functions of a variable, called a parameter. For example,

A common example occurs in kinematics, where the trajectory of a point is usually represented by a parametric equation with time as the parameter.
Ellipse
It is the locus of a point which moves in such a way that the sum of it's distance from two focus is a constant which is equal to 2a.
An ellipse in canonical position (center at origin, major axis along the X-axis) with semi-axes a and b can be represented parametrically as


- The equation of an ellipse whose major and minor axes coincide with the Cartesian axes is
 This can be explained as follows:
This can be explained as follows:
If we let 
- Then plotting x and y values for all angles of θ between 0 and 2π results in an ellipse (e.g. at θ = 0, x = a, y = 0 and at θ = π/2, y = b, x = 0).
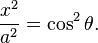

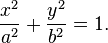
This means any noncircular ellipse is a compressed (or stretched) circle. If a circle is treated like an ellipse, then the area of the ellipse would be proportional to the length of either axis (i.e. doubling the length of an axis in a circular ellipse would create an ellipse with double the area of the original circle).
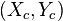 is the center of the ellipse, and
is the center of the ellipse, and 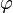 is the angle between the
is the angle between the  -axis and the major axis of the ellipse
-axis and the major axis of the ellipse
Focus
The distance from the center C to either focus is f = ae, which can be expressed in terms of the major and minor radii:
 ) is
) is
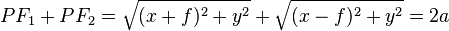 .
.
Eccentricity
The eccentricity of the ellipse (commonly denoted as either e or ) is
) is
Ellipse ,It'a Algebraic and Parametric Equation and Application in physics1: http://t.co/VV0pSNCLKh via @YouTube
— Abraham Malik (@brhmmlk93_malik) February 14, 2015

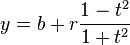
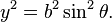




No comments:
Post a Comment